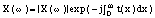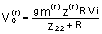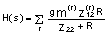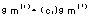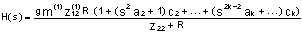FC Coding is
One step from 1st Principles to Solution!

Home

Increased Productivity Example #2



Arbitrary Equalization with Simple LC Structures

Robert Kost, MEMBER IEEE, and Philip Brubaker

Abstract-Equalization for magnetic recording with LC filters was reported in 1963 [1], and since then many other approaches have been used to alter the readback signal to reduce error. These ideas have been extended to arbitrary input-arbitrary output fillers which are realized as LC structures without mutual inductance. An asymmetrical signal from an isolated pulse is equalized to become optimum in the linear Van der Maas sense [2]. The change in the signal to noise ratio as a result of equalization is computed as a function of pulse slimming.

INTRODUCTION

Implicit in efficient utilization of a communication channel is proper signal design. This can be illustrated by noting that the Nyquist limit cannot be achieved for an arbitrary symbol (pulse) shape, but only for symbols that have the proper zero crossings. In general then, equalization will be required to effectively use the available bandwidth. If the readback

Time function of isolated readback signal

Fig. 1a. Time function of isolated readback signal

Magnitude function of isolated readback signal

Fig. 1b. Magnitude function of isolated readback signal.

signal can be viewed as coming from a linear system which has a restricted set of input signals, a linear filter can be used to remove intersymbol interference. The conditions under which this notion is valid were reported in 1969 and 1978 [3,4]. If the equalizer is viewed as a windowed inverse filter, it is clear, at least in principle, that the readback signal can be altered to more effectively utilize the bandwidth. This is a report of a frequency domain design of an equalizer with the input frequency function derived directly from an isolated readback pulse. The output frequency function is the linear Van der Maas quasi-optimum approximation. The equalizer's pole-zero constellation is determined by using a nonlinear optimization routine available in the PROSE language [5]. The filter is realized so that mutual inductance is not possible [6]. Additionally, the realization can be accomplished with closed form expressions without recourse to insertion loss filter design. Since the equalizer affects the signal to noise ratio, a discussion of the minimum signal to noise change is included.

Input Signal Acquisition

The Fourier transform (FT) of an isolated readback pulse is computed by taking the Fourier transform of signal samples (FT*) [7]. Since the time data are rectangularly windowed and band limited the FT* is a least-square fit to FT [8]. Because of this, FT* is least-square fitted to estimate FT. The time function, t(ω), is obtained by taking the negative derivative of the phase function. The input frequency function is described in the following way:

Fourier Transform of Input Signal            (1)

The magnitude and the time functions are shown in Fig. 1. It is interesting to note that there appears to be a discontinuity at the origin in the phase function. No fundamental reason was found for this.

Output Signal Design

For systems that use peak detection, loosely stated requisites for a signal are that it be narrow and the sidelobe disturbance be low. These were the criterion that were used to design the pulse that Vakman refers to as quasi-optimal [2].

This pulse was designed to give the narrowest pulse for a specified bandwidth and sidelobe suppression. The width of the pulse (distance between zero crossings) for 60 dB sidelobe suppression is 15.48/WB where WB, is the bandwidth.

FILTER APPROXIMATION

It should be noted that since this is going to be an LC filter realization, the group delay of the filter is completely a function of the pole locations. The zeros do not contribute to the filter group delay. With this in mind, the design process is broken into three stages:

1) adjust the filter pole locations only until the output frequency function's time function, t(ω), is approximately constant.

2) adjust the zero locations (while holding the pole locations constant) until the magnitude of the output frequency function is satisfactory.

3) adjust all critical frequencies simultaneously while constraining the maximum group delay error.

Consider the following definitions:

X(ω) = input frequency function

Hj(ω) = equalizer transfer function at j’th iteration

Yj(ω) = equalizer transfer function at j’th iteration
Yd(ω) = equalizer transfer function at j’th iteration

C(ω) = equalizer transfer function at j’th iteration

where:

Yj(ω)= Hj(ω) X(ω)                   (2)

The objective function, θj, to be minimized is defined to be:

Θj = ΣkEj2 (ωk)

where
Error function                   (3)

and ωk are discrete values of ω.

The equalizer's pole-zero constellation is obtained by iteratively adjusting the root locations until the objective function is minimized. The calculation is done by a nonlinear optimization routine available on PROSE, while the filter is being driven by the frequency function of an isolated pulse.

FILTER REALIZATION

During the approximation portion of the design, terminated reactance two port realization conditions were carefully observed. This will guarantee that the equalizer can be built as an LC filter. These realizability conditions, however do not guarantee a filter without mutual inductance or negative element values. In addition to these problems, the LC structures often have impractical element values. All of these problems can usually be avoided by the synthesis approach that is now going to be described.

The basic topology to be used is referred to as "additive amplification" [9,l0,11,12]. This topology involves injecting currents into nodes of an LC ladder filter. The output voltage of this design is the sum of the voltages due to the individual current sources, hence the name "additive amplification."

Consider a voltage-controlled current source driving node r of an all-pole singly-terminated LC filter. The output voltage due to this single-current source is well known and is given by [13]:

Output Volt at Node R                  (4)

where V(r)o is the voltage across R due to current sourcing at node r and gm is transconductance of the current source.

Using equation (4), the transfer function of the filter will be:

Filter Transfer function                  (5)

The transconductance of the r'th source can be related to the transconductance of the 1'st source (unterminated end of LC filter) by a multiplicative constant:

Transconductance Source                  (6)

Also, the transfer impedances between the nodes and the output can be related. Using these ideas in equation (5) yields:

Transfer Impedance at Source      (7)

where k is the number of nodes being driven by current sources and ak are constants that relate the component values of the filter.

It is clear that the transfer function of this realization is related to the LC ladder transfer function by a multiplicative even polynomial. This results in k-1 unknowns and k-1 linearly independent equations.

Since all-pole LC filters are guaranteed not to contain mutual inductance and the element values are nearly always positive and do not change by more than about a factor of ten, this realization procedure circumvents many of the problems attendant with insertion loss design.

Two filters with the same pole-zero constellation are shown in Fig. 2. The first was designed with standard insertion loss techniques while the second is similar to Fig. 6-11 in [12]. The improvement, as far as practical implementation goes, in the "additive amplifier" approach is self-evident.

The all-pole filter can be realized by using insertion loss theory (the driving point impedance is the ratio of the even and odd parts of the transfer function numerator) or closed form expressions can be derived. The closed form expressions can be derived by expressing the transfer function in terms of its pole locations and in terms of its element values. By equating the coefficients of the denominator of these two transfer functions, a set of linear equations will be formed that will result in closed form expressions for the element values in terms of the pole locations.

Comparison of an insertion loss realization

Fig. 2a. Comparison of an insertion loss realization
          b. With a multi-input realization


FIGURE OF MERIT

An important consideration for an equalizer design involves the change in the signal to noise ratio (SNR) introduced by the equalizer. Here the SNR is defined as the peak signal to the rms noise voltage. The figure of merit (FM) of the filter is the ratio of the input to the output SNR expressed in dB. The computation was done numerically with the input signal being Lorentz, the output signal being Van der Maas and the noise power spectral density was taken directly from a disc. The FM as a function of the ratio TM/PW50 is shown in Fig. 3 where TM is one-half the distance between the zero slope points on the Van der Maas (VDM) time function.

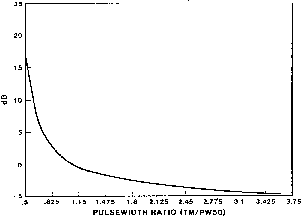
Figure of merit

Fig. 3. Figure of merit

FILTER DESIGN EXAMPLE

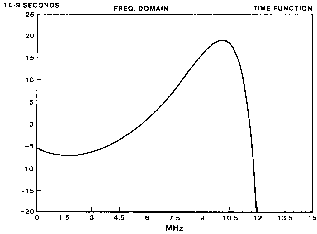
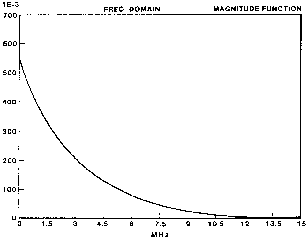
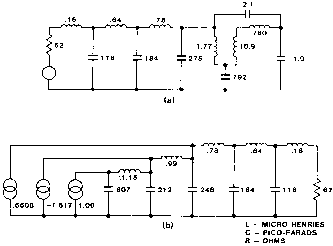
An equalizer to remove intersymbol interference in the time derivative of the slimmed output is now designed to illustrate the ideas discussed thus far. The input signal has a PW50 of about 110 ns and the output VDM frequency function has a cutoff frequency of 12.36 MHz. Initially, the pole locations of the filter were adjusted to equalize the group delay to 10 MHz. This resulted in a time function error (deviation from a constant) of 1.5 ns. Then the zeros were adjusted to minimize the magnitude error. A SPICE analysis of the equalizer showing the input and the output are shown in Fig. 4.

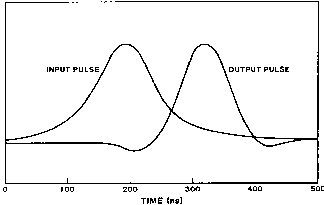
Spice simulation of example design

Fig. 4. Spice simulation of example design

CONCLUSIONS

During the process of developing this design approach, it became clear that a more appropriate approach would be to specify the objective function in the time domain. This would completely circumvent the need for having precise information about the group delay, for example. Only a modest change is required to change the procedure described here into a time domain design.

ACKNOWLEDGMENTS

Special thanks go to Mr. Don Huber and Dr. Maung Gyi for their significant contributions, and to Mr. Frank Sordello for his support.

REFERENCES

[1] H.M. Sierra, "Increased Magnetic Recording Read-back Resolution by Means of a Linear Passive Network", IBM Journal, Jan. 1963.

[2] D.E. Vakman, Sophisticated Signals and the Uncertainly Principle in Radar, Springer-Verlag New York Inc., 1968.

[3] J.C. Mallinson and C.W. Steele, 'Theory of Linear Superposition in Tape Recording', IEEE Transactions on Magnetics, Vol. MAG-5, No. 4, Dec. 1969.

[4] B.K. Middleton and P.L. Wisley, 'Pulse Superposition and High Density Recording', IEEE Transactions On Magnetics, Vol. MAG-14, No. 5, Sept. 1978.

[5] PROSE, Inc., Palos Verdes Estates, CA 90274.

[6] T. Fujisawa, 'Realizability Theorem for Mid-series or Mid-shunt Low-pass Ladders Without Mutual Induction', IRE Transaction-Circuit Theory, Dec. 1955.

[7] A.V. Oppenheim and R.W. Schafer, Digital Signal Processing, Prentice Hall, Inc., 1975, p 21.

[8] Korn and Korn, Malhemafical Handbook for Scientist and Engineers, McGraw Hill, 1968, pp 134-136.

[9] W.C. Percival, Thermionic Valve Circuits, British Patent 460562, July 1935.

[10] E.L. Ginrton, W.A. Hewlett, J.H. Jasberg and J.D. Noe, Distributed Amplification, Proc IRE, vol 36, pp 956-969, Aug. 1948.

[11] P.H. Rodgers and L.H. Enloe, Transistor Distributed Amplifier, U.S Signal Corps Contract DA-36-039 SC-75021, March 1958.

[12] J.M. Pettit and M.M. McWhorter, Electronic Amplifier Circuits, McGraw Hill, 1961, pp 147-163.

[13] G.C. Temes and J.W. LaPatra, Introduction to Circuit Synthesis and Design, McGraw Hill, 1977, pp 157-159.

Manuscript received March 23, 1981. Paper 37-8 presented at the 1981 INTERMAG Conference, Grenoble, France, May 12-15. The authors are with the Recording Technology Center, Memorex Corporation, Santa Clara, California 95052.

This Pulse Slimming is another increased productivity example do to using Calculus (level) programming.

Website

visit https://goal-driven.net for Match-n-Freq app. to reproduce the results discussed in this article.


HTML code for linking to this page:


<a href=""><img style="float:left; width:100px" src="https://goal-driven.net/image/pulse-pic5.png"/> <strong>Pulse Slimming for magnetic recording</strong> </a> with LC filters.

< < Back

Next > >
 
Valid CSS! Calculus (level) Problem-Solving for Engineers & Scientists

Textbooks - Parameter Estimation 4 ODE/PDE - Signal Analysis / Spectral Estimation - Body Plasma - Solar Cell
Increasing Productivity Examples: AC Motor Design - Matched Filters - Pulse Slimming / InterSymbol Interference - Pilot (safe) Ejection - PharmacoKinetics Simulation - Business Strategies & War Gaming - BVP - Implicit Equations